Data Models (DataSets, Cells, Points and their Attributes)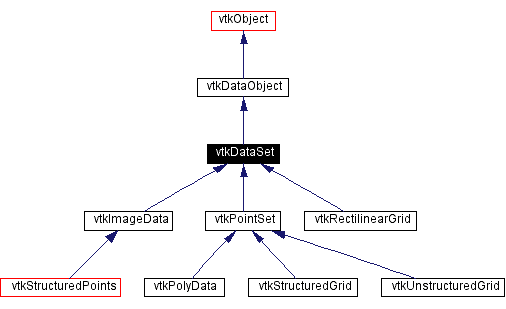
DataArrays as well as FieldData lack the complexity needed to describe
geometrical properties of objects we want to visualize. For this purpose
VTk provides 5 more sophisticated objects ( data models, all are
descendants of vtkDataSet abstarct class, see picture above) -
vtkImageData, vtkRectilinearGrid, vtkStructuredGrid, vtkPolyData,
vtkUnstructuredGrid. Only classes derived from vtkDataSet class can be
visualized by VTK.
Internally vtkDataSet consists of points and cells and any number of
associated data (attributes). Points are the coordinates of models'
vertices. Cells describes the way the vertices are connected with each
other. Individual point or cell is indexed and identified by its
(point's or cell's) Id number. You may think about points as a
two-dimensional array with 3-columns (x-, y- and z- coordinate) and the
point's id being the row index in this array. The cells looks like a
list whose elements are arrays consisting of point's ids of cell's
vertices. People with mathematical background tend to think that cells
are simplexes but this is not true: the cell can have arbitrary topology
and the number of its verices does not correspond with cell's
dimensionality. Cells are just geometrical object with "simple"
(whatever this means) topology.
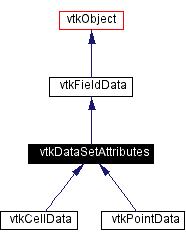
Associated data falls into two classes: the one associated with cells
or points. They are of different classes vtkPointData and vtkCellData
but through vtkDataSetAttributes class they are derived from
vtkFieldData class so you can manipulate attribures through FieldData's
methods.This means that you can pass arbitrary DataArrays as attribute
data. The examples of attributes are the values of scalar field at the
nodes of finite-difference grid (point's data) or normals' directions of
2D surface (cell's data).
vtkDataSet defines methods for getting/setting cell's or point's
attributes and the means to find the local connectivity of points and
cells (i.e. bidirectional mapping between points' ids and cells' ids
through Cells list). Note, however, that there is no unified interface
to set and query the values of Points and Cells. It is done
intetntionally because some of DataSet implementations does not require
this information and it can be calculated on the fly when needed.
For example, vtkImageData is a 3-dimensional equally-spaced rectangular
grid so its topology is fairly simple. As its name suggests its main
purpose to store image data (even 3-dimensonal images which for
example medical tomography devices do output). Points' coordinates
are the indexes of image's pixel so they can be derived from point's id,
width and height of the image. All cells are the cubes with length one
so it is trivial to find the point's ids of vertices of these cubes.
Color and alpha data of vtkImageData can be accessed as
PointAttributes. Although vtkImageData provides an interface of its own
to access RGBA values (different from vtkFieldData's one), RVTK users
can apply "[]<-" and "[]" notation to do the same thing. You can also
use ImageData(R-matrix) to create and initialize vtkDataImage instance.
The R-matrices can have up to 4 dimensions, the first 3 index components
are x,y,z coordinates (they are tagged as "x", "y", "z") and the fourth
is the "color" (tagged as "c").
vtkRectilinearGrid is slightly different from vtkImageData in that the
grid is not equally spaced. Nonetheless both Points and Cells are
calculated (not stored) too.
Descendants of vtkPointSet abstract class need explicit information
about points' coordinates. This is done through Set/GetPoints methods
which work with vtkPoints classes. vtkPoints in its turn has
Set/GetDataArray methods which work with vtkDataArray instances. Now we
can create a vtkPolyData model and assign coordinates to its vertices.
vtkPolyData()->model
vtkPoints()->Points
Points$SetData(p)
model$SetPoints(Points)
vtkPolyData represents a geometric structure consisting of vertices,
lines, polygons, and triangle strips. vtkUnstructuredGrid is most
general DataSet class which can consist of arbitrary cells with
arbitrary dimensions. Both of them require the Cells data to be set
explicitely but this is achieved in different ways. Note that
vtkStructuredGrid (the third descendant of vtkPointsSet) which
represents distorted grid topologically equivalent to rectilinear grid
still calculates cells implicitely.
For vtkPolyData instance (class most widely used by VTK applications)
the cells data can be set independently for 0D, 1D and 2D cells with the
methods:
$SetVerts(.v = vtkCellArray())
$GetVerts()
$SetLines(.l = vtkCellArray())
$GetLines()
$SetPolys(.p = vtkCellArray())
$GetPolys()
$SetStrips(.s = vtkCellArray())
$GetStrips()
So vtkPolyData with only Verts set represents a points' cloud, with
only Lines set - lattice, with only Polys or Strips - surface.
vtkPolyData allowed to have pices of different dimensions so this
methods can be used simultaneously on the same vtkPolyData object to
define these pieces.
vtkCellArray allows the user to build the cells from bottom up
(i.e. adding cell by cell with $InsertNextCell... methods) or
define the structure at once with the method $SetCells(.ncells, .cells =
vtkIdTypeArray()). ".ncells" is the number of cells defined in
the ".cells" integer array. The format of ".cells" array is the
following: at the beggining is the number of points in the first cell,
then the ids of all points in this cell and this is repeated for all
other cells.
For example, we will create the tetrahedra with the coordinates we have
defined earlier.
vtkCellArray()->Faces
Faces$SetCells(4,f)
model$SetPolys(Faces)
We can also associate data with this model (both cells' and points')
model$GetCellData()$SetScalars(DoubleArray(1:4))
model$GetPointData()$SetScalars(DoubleArray(1:4))
Note that through the VTK pipeline the objects travels by reference not
by value, so actually no data copying takes place. So for example if we
assign new value to components of vtkDataArray p (p[1,1]<-1) the
geometry of the model will be updated too. So the equality
p[1,1]==model$GetPoints()$GetData()[1,1] is always true.
<Previous Next>


